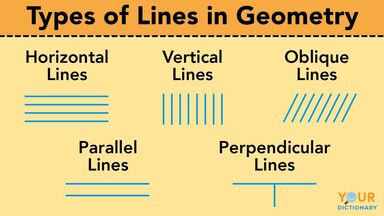
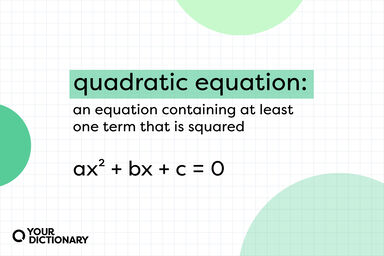Linear Independence Definition

noun

The property of a set of vectors of having no linear combinations equal to zero unless all of the coefficients are equal to zero.

American Heritage

(algebra) The state of being linearly independent.

The linear independence of a set of vectors can be determined by calculating the Gram determinant of those vectors; if their Gram determinant is zero, then they are linearly dependent, and if their Gram determinant is non-zero, then they are linearly independent. Incidentally, the same Gram determinant can be used to calculate the hyper-volume of a hyper-parallelepiped (whose edges which "radiate" from an "origin" vertex are described by the vectors).

Wiktionary