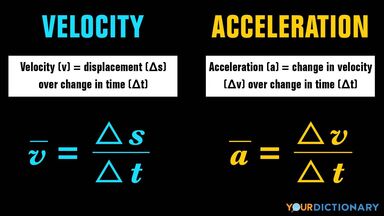
If the total resistance against which the train is maintained in motion with an instantaneous velocity of V feet per second is R, the rate at which energy is expended in moving the train is represented by the product RV, and this must be the rate at which energy is supplied to the train after deducting all losses due to transmission from the source of power.
Then Ob is the velocity of the point b in magnitude and direction, and cb is the tangential velocity of B relatively to C. Moreover, whatever be the actual magnitudes of the velocities, the instantaneous velocity ratio of the points C and B is given by the ratio Oc/Ob.
Having obtained the set of instantaneous centres for a chain, suppose a is the fixed link of the chain and c any other link; then O,,,is the instantaneous centre of the two links and may be considered for the instant as the trace of an axis fixed to an extension of the link a about which c is turning, and thus problems of instantaneous velocity concerning the link c are solved as though the link c were merely rotating for the instant about a fixed axis coincident with the instantaneous axis.