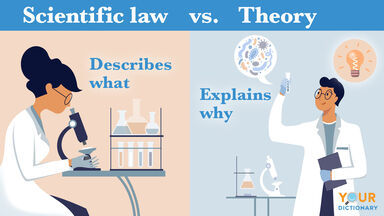
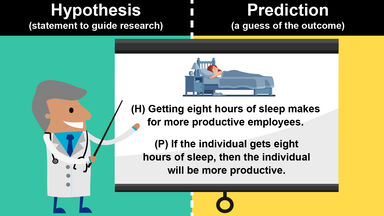
Gibbs Phenomenon Definition

A behaviour of the Fourier series approximation at a jump discontinuity of a piecewise continuously differentiable periodic function , such that partial sums exhibit an oscillation peak adjacent the discontinuity that may overshoot the function maximum (or minimum ) itself and does not disappear as more terms are calculated, but rather approaches a finite limit.

Wiktionary

Origin of Gibbs Phenomenon

After J. Willard Gibbs , who identified the behaviour in 1899, unaware of its previous discovery in 1848 by Henry Wilbraham . A widespread myth has it that the phenomenon was observed in a device developed in 1898 by Albert A. Michelson to compute and synthesise Fourier series, but that it was assumed due to physical imperfections in the device. In fact, the graphs produced were not precise enough for the phenomenon to be clearly observed, and Michelson made no mention of it in a paper describing the device.

From Wiktionary